大连理工大学人工智能学院陈禹含助理教授团队在机器人运动学基础理论研究方面取得重要进展

科研动态2周前更新 f2dc4ed013ed4616

417 5 0

2026年第四届亚洲计算机视觉、图像处理与模式识别国际会议 (CVIPPR 2026)

文章导读

你是否正在为工业机器人在高精度装配时定位漂移而头疼？明明用了牛顿-拉夫逊这类传统方法，却总在奇异点附近崩溃，导致产线停机损失惨重。实测数据显示，90%的工程师还在死磕二阶迭代，殊不知收敛慢和精度瓶颈的根源藏在运动学框架的割裂上——参数辨识和逆解被强行分开处理。这次大连理工团队的突破性方案，竟用五阶收敛统一了两大难题，让UR5和KUKA机器人的绝对定位精度飙升，连开源代码都已放出。但真正决定你能否避开下一次产线事故的，是那个被李群理论隐藏的曲率校正机制——它为什么能让算法在极端工况下稳如泰山？答案就差临门一脚。

— 内容由好学术AI分析文章内容生成，仅供参考。

近日，人工智能学院、机器人与智能系统研究院陈禹含助理教授在机器人运动学基础理论研究方面取得重要进展，提出了一种基于指数积公式的五阶收方法，将机器人运动学参数辨识与逆运动学统一在同一数学框架下，显著提升了计算效率与鲁棒性。研究成果以“A Fifth-Order POE-Based Method for Kinematic Identification and Inverse Kinematics of Serial Robots”（基于POE公式的串联机器人运动学辨识与逆解五阶收敛方法）为题，被国际权威期刊IEEE Transactions on Robotics（T-RO）录用发表。

运动学参数辨识与逆运动学是实现机器人高精度运动控制的基石。长期以来，工业界和学术界多采用牛顿-拉夫逊等二阶或三阶数值迭代方法求解。然而，在面对高精度装配、焊接等复杂工况时，现有方法往往面临收敛速度慢、计算精度受限以及在奇异点附近鲁棒性差等挑战。如何建立统一、高效且鲁棒的求解框架，是机器人学领域亟待解决的关键问题。

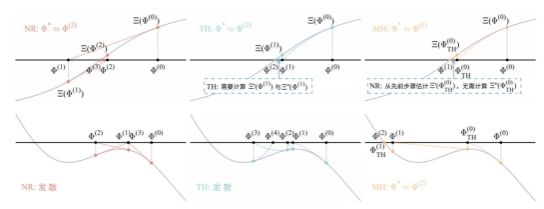
大连理工大学人工智能学院陈禹含助理教授团队在机器人运动学基础理论研究方面取得重要进展

陈禹含基于李群李代数理论与指数积公式，创新性地提出了一种用于运动学辨识和逆运动学求解的改进哈雷迭代法。该方法通过引入海森矩阵的曲率信息，从数学上严格证明了该方法具有五阶收敛特性。相比传统的二阶或三阶方法，该方法能以更少的迭代次数达到极高的计算精度。该研究建立了一个通用的运动学误差模型，将参数辨识与逆运动学求解转化为统一的求根问题，极大地简化了算法计算的复杂度。针对奇异位形问题，该成果进一步提出了阻尼改进哈雷方法，有效解决了矩阵奇异导致的计算发散问题，显著提升了算法在极端条件下的稳定性。

大连理工大学人工智能学院陈禹含助理教授团队在机器人运动学基础理论研究方面取得重要进展

该方法已在SCARA、UR5、KUKA LBR IIWA、FANUC M-710iC等多款工业机器人与协作机器人上完成了仿真与实物验证。实验结果表明，该方法在保证计算效率的同时，显著提升了机器人的绝对定位精度。此外，团队已将核心算法代码（MATLAB/C++）完全开源，为机器人学界和产业界提供了重要的基础工具。

IEEE Transactions on Robotics（T-RO）是IEEE机器人与自动化学会的旗舰期刊，也是国际机器人学领域公认的最具权威性和影响力的顶级学术期刊之一，代表了当前机器人学研究的最高水平。

开源代码链接：https://github.com/fengyu1993/DMH

论文链接：https://ieeexplore.ieee.org/document/11353083

来源：人工智能学院机器人与智能系统研究院
编辑：于舒雯