电子科技大学数学学院王朝霞副教授在Mathematische Annalen期刊发表研究成果
文章导读
你是否想过,一个秋千的摆动或一次药物注射背后,竟隐藏着复杂的数学规律?当传统方法无法破解非光滑系统的周期之谜,电子科技大学王朝霞副教授携手多所高校学者,在国际顶级数学期刊Mathematische Annalen发表突破性成果,首次提出判断具有状态脉冲的Rayleigh–Liénard系统周期解唯一性的全新准则,并成功应用于脉冲单摆与弹簧振子模型。这项研究为力学、生态乃至医学治疗系统提供了关键理论支撑,揭开非光滑动力系统中“极限环唯一性”的神秘面纱。
— 内容由好学术AI分析文章内容生成,仅供参考。
近日,数学科学学院王朝霞副教授与中南大学陈和柏教授、金杰博士,以及上海交通大学肖冬梅教授合作,在Mathematische Annalen期刊发表了题为“On the uniqueness of periodic solutions for a Rayleigh-Liénard system with impulses”的论文,针对具有状态脉冲的Rayleigh–Liénard系统,提出了一套判别周期解唯一性的准则。
具有状态脉冲的Rayleigh–Liénard系统在现实世界中具有广泛的应用,可用于描述力学系统、生态系统以及疾病治疗系统等。例如,施加恒定推力的秋千往复运动、药代动力学中的固定剂量给药机制,均可视为状态依赖的脉冲系统。由于系统具有非光滑性,传统适用于 C¹ 平面动力系统的极限环唯一性方法在此类系统中不再适用,因此目前关于状态依赖脉冲动力系统的大范围穿越极限环研究仍较为稀少。
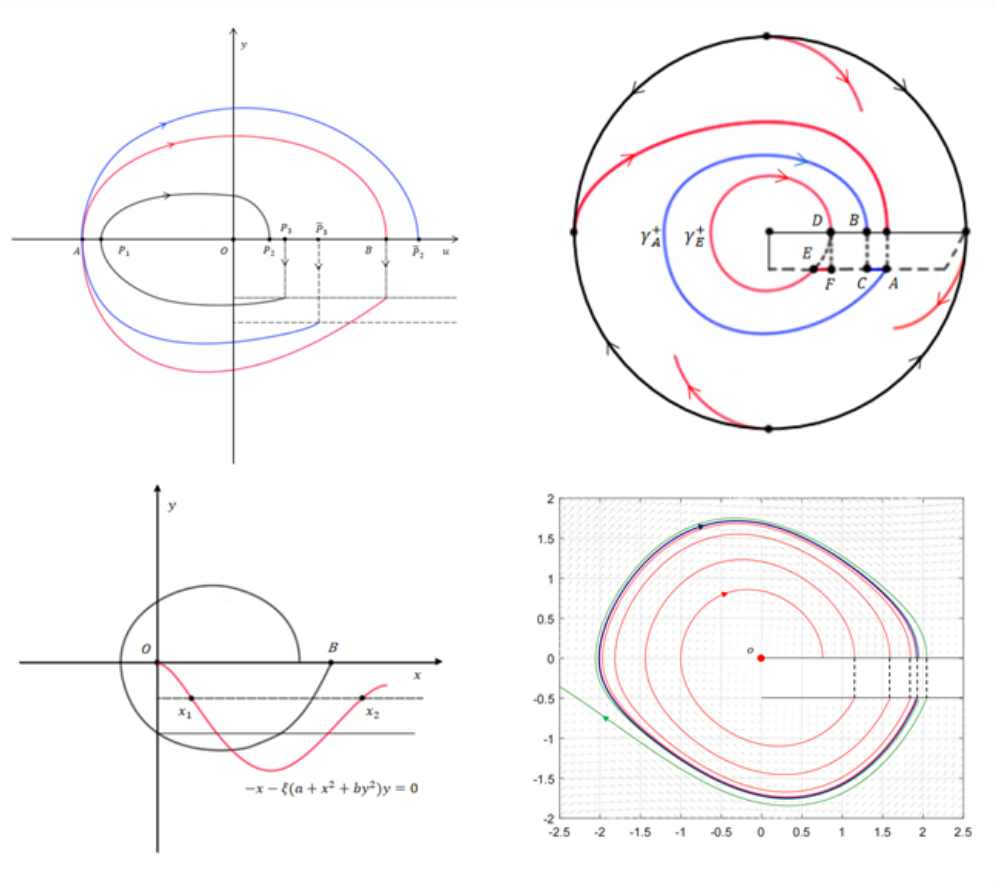
该文提出了一套用于判别脉冲动力系统穿越极限环的准则,并基于该准则,分别证明了状态依赖型脉冲单摆与状态依赖型脉冲弹簧振子周期解的唯一性。
王朝霞,副教授,博士。2011年获四川大学理学博士学位,同年加入电子科技大学数学科学学院。研究方向为微分方程与动力系统,相关成果发表在Mathematische Annalen、Journal of Differential Equations、Physica D、Discrete and Continuous Dynamical Systems等期刊上。主持国家自然科学基金项目2项。
论文链接:https://doi.org/10.1007/s00208-024-02996-5
© 版权声明
本文由分享者转载或发布,内容仅供学习和交流,版权归原文作者所有。如有侵权,请留言联系更正或删除。
相关文章

暂无评论...