电子科技大学数学学院Jonas KAHN教授在Proceedings of the London Mathematical Society发表学术论文
文章导读
测地线会“卡在”慢速路上吗?电子科大Jonas KAHN教授团队十年磨一剑,在顶级数学期刊《伦敦数学会会刊》重磅破解Kendall猜想:平面泊松道路中的测地线从不停顿——除端点外,它们坚决避开所有低速路径!本文首次严谨证明该随机度量空间(豪斯多夫维数4)的深层逻辑:最短路径由行驶时间定义,且模型可无缝扩展至高维,颠覆传统随机几何局限。数学前沿突破在此,速览如何重塑你对空间维度的认知!
— 内容由好学术AI分析文章内容生成,仅供参考。
近日,数学科学学院Jonas KAHN教授与瑞士联邦理工学院 Guillaume BLANC 博士和巴黎萨克雷大学Nicolas CURIEN教授合作,在顶级期刊《Proceedings of the London Mathematical Society》上发表了题为“Geodesics in planar Poisson road random metric”的论文,对平面泊松道路度量(planar Poisson road metric)中的测地线进行了深入分析,证明了KENDALL十年前提出的一个猜想:这些测地线在行进途中不会停顿,即除了在端点处,它们不会使用速度任意小的道路。

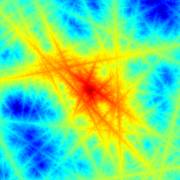
平面泊松道路度量是一个随机度量空间,它在平移、旋转和缩放下保持不变,并且其中的测地线会发生汇聚(该度量空间与R²同胚,其豪斯多夫维数为4;若先将每条测地线端点附近的小球去掉,再取所有剩余部分的并集,其豪斯多夫维数为 1。)该度量空间的构造方式是:在平面上随机投放带有固定速度v的直线(速度越慢的直线数量越多,因此任意方形区域内都有无穷多条慢速直线相交)。该空间的度量由从一个点到另一点的最短行驶时间定义。
平面泊松道路度量的一个优势在于,它可以自然推广到更高维空间,而典型的随机几何模型通常难以做到这一点。另一方面,本文的结果也表明,其平面行为与其他已深入研究的平面随机度量具有相似性。

Jonas KAHN,教授,博士,国家级青年人才。曾先后获得法国奥赛大学(Orsay University)和荷兰莱顿大学(Leiden University)博士学位。2008年起在法国国家科学研究中心(CNRS)工作,2022年加入电子科技大学数学科学学院。研究兴趣广泛,曾与物理学家、生物学家、计算机科学家和神经科学家合作研究相关课题。其专业领域包括随机几何、量子统计、压缩感知等。在《Annals of Probability》《Annals of Statistics》《Annals of Applied Probability》《Physical Review A》等刊物上发表学术论文35篇。
论文连接:https://londmathsoc.onlinelibrary.wiley.com/doi/10.1112/plms.70070
© 版权声明
本文由分享者转载或发布,内容仅供学习和交流,版权归原文作者所有。如有侵权,请留言联系更正或删除。
相关文章

暂无评论...