电子科技大学数学学院博士生潘帅在Mathematics of Computation上发表研究成果
文章导读
当传统Fourier变换在复杂结构散射问题中遭遇瓶颈,电子科技大学博士生潘帅联手国际顶尖学者给出了惊艳解法!他们提出的FTH-MS算法通过独创的光滑单位分解策略,将困扰学界多年的时域波动方程难题拆解为可精准计算的序列。这项发表于《Mathematics of Computation》的突破性研究,不仅巧妙避开Helmholtz方程的特征值陷阱,更实现了对复杂散射体的高精度计算。想知道他们如何用全新算法打破计算壁垒,将计算量大幅降低的同时向三维问题迈进?这场计算数学的革新正在重新定义波动方程求解的边界。
— 内容由好学术AI分析文章内容生成,仅供参考。
近日,数学科学学院博士研究生潘帅与浙江大学包刚教授、中国科学院数学与系统研究院殷涛副研究员、美国加州理工学院Oscar Bruno教授合作,针对时域波动方程问题,提出了一种基于Fourier变换和积分方程的高精度多重散射算法(FTH-MS)。相关成果被《Mathematics of Computation》期刊接收。
复杂结构多重散射问题的分析与计算一直是散射问题研究领域的难点问题,陷波结构导致的共振使得Fourier变换通常无法直接用于求解时域问题。该论文引入一种光滑单位分解策略,将波动方程的解分解为一系列开弧子问题的多重散射序列。这些子问题在频域中唯一可解,从而有效地避免了Helmholtz方程内问题的特征值问题,极大地扩展了Fourier变换的适用性。
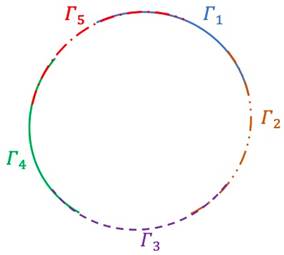
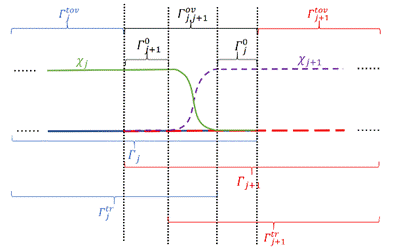
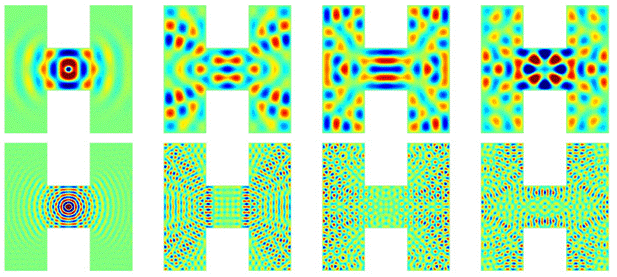
该研究是对多重散射算法(O.P. Bruno, T. Yin, Math. Comput. 93(346) (2024) 551-587)的进一步推广。与原算法相比,新的方法可以对边界进行任意分解,因此可以用于复杂散射体的计算。同时,文章对开弧子问题涉及的边界值和积分方程求解的密度函数在边界上的奇性进行了细致的刻画,结合余弦变换可以实现高精度计算,在减少计算量的同时也更容易推广到三维问题。
论文链接:https://doi.org/10.1090/mcom/3946
© 版权声明
本文由分享者转载或发布,内容仅供学习和交流,版权归原文作者所有。如有侵权,请留言联系更正或删除。
相关文章

暂无评论...